DeepSeek 于 2025 年 11 月 27 日发布 DeepSeekMath-V2 模型,并开源到 HuggingFace。该模型构建于 DeepSeek-V3.2-Exp-Base 之上,模型参数为 685B。
大型语言模型在数学推理方面取得了显著进展,这不仅是人工智能的重要试验场,若能进一步发展,还将对科学研究产生深远影响。通过利用奖励正确最终答案的强化学习来扩展推理能力,大语言模型(LLM)在短短一年内从表现不佳发展到在 AIME 和 HMMT 等定量推理竞赛中达到饱和状态。然而,这种方法面临着根本性的局限性:追求更高的最终答案准确率并未解决一个关键问题:正确的答案并不保证推理过程是正确的。此外,许多数学任务(如定理证明)需要严谨的逐步推导而非数值答案,这使得基于最终答案的奖励机制不再适用。为了突破深度推理的极限,我们认为有必要验证数学推理的全面性和严谨性。自我验证对于扩展测试时计算(test-time compute)尤为重要,特别是针对那些没有已知解的开放性问题。为了实现可自我验证的数学推理,我们研究了如何针对定理证明训练一个准确且忠实的大模型验证器。随后,我们使用该验证器作为奖励模型来训练证明生成器,并激励生成器在定稿之前尽可能多地识别并解决自身证明中的问题。随着生成器变得更强,为了维持生成与验证之间的差距,我们提出扩展验证计算规模,自动标注那些难以验证的新证明,从而创建训练数据以进一步改进验证器。我们的最终模型 DeepSeekMath-V2 展示了强大的定理证明能力,在扩展测试时计算的情况下,在 IMO 2025 和 CMO 2024 中获得了金牌级分数,并在 Putnam 2024 中取得了近乎完美的 118/120 分。尽管仍有许多工作要做,但这些结果表明,可自我验证的数学推理是一个可行的研究方向,可能有助于开发能力更强的数学 AI 系统。
2. 评估结果
以下是在 IMO-ProofBench(由开发 DeepThink IMO-Gold 的 DeepMind 团队开发)以及近期的数学竞赛(包括 IMO 2025、CMO 2024 和 Putnam 2024)上的评估结果。
IMO-ProofBench
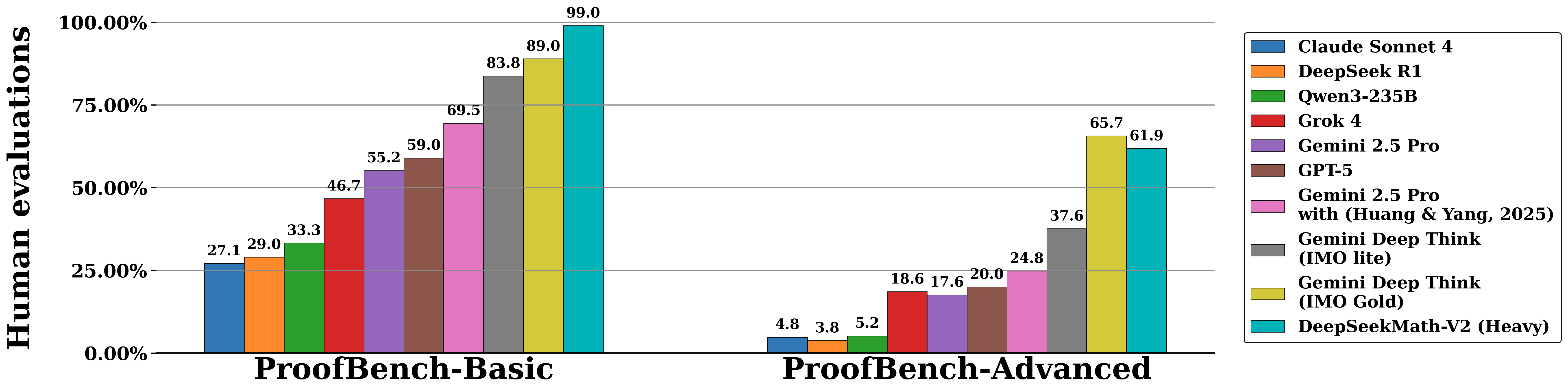
数学竞赛

3. 快速开始
DeepSeekMath-V2 构建于 DeepSeek-V3.2-Exp-Base 之上。 关于推理支持,请参阅 DeepSeek-V3.2-Exp GitHub 仓库。